Examples of using AutoEZ have been created from time to time to address questions raised on various forums and reflectors. This is a collection of such examples, in some cases slightly edited. Step by step instructions are omitted to maintain brevity.
Modeling Fan Dipoles and OCF Dipoles
Three new models have been added to the AutoEZ samples folder as of maintenance release v. 2.0.6.
With model "Fan Dipole Splayed Elements.weq" you can set variables to easily configure the wires like this, for example, which might represent a fan strung between two supports with a "catenary sag" in the center.
Change the variables another way to get this kind of configuration, inverted vees held up by a center support and two shorter end supports.
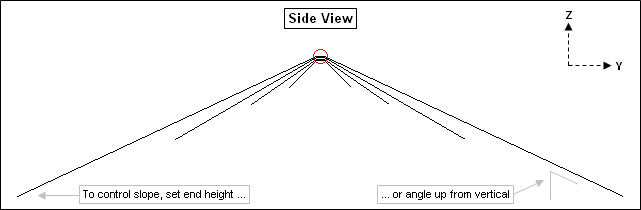
To control the slope (if any) for each side of each element you can set either the height of the outer end or the angle of the wire up from vertical. Whichever you enter will be used along with the total wire length and center height to generate the correct coordinates in the wires table. In addition, the corresponding "other" value (angle or end height) will be shown. The two sides need not have the same slope.
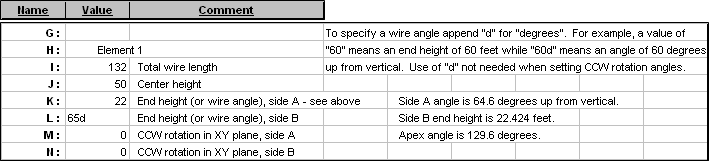
Here is an extract from the Variables sheet tab showing how you control the first (top) element. Other groups of variables, not shown, control the other elements. The number of elements in the model is adjustable from 1 to 6. (Set the number of elements first, then set other groups of variables as appropriate.)
If you would prefer to work with meters or inches instead of feet use the Change Units button (with the "retain formulas" option) and then reset the variable values as desired.
You can also rotate the outer ends of one or more elements in the XY plane, perhaps to increase the separation between wires or take advantage of available supports. Here is a top-down view of a set of inverted vees with the outer ends of the 80m element rotated in a somewhat arbitrary manner, just for illustration. Side A of the 80m element has been rotated 20° CCW in the XY plane and side B has been rotated 330° (or -30°) CCW.
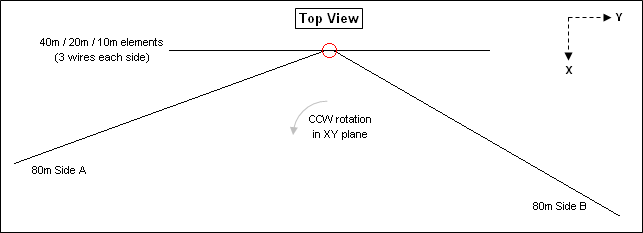
As you change variables be sure to frequently use the View Ant button to verify that the wires of the model are positioned as you intended. Make sure that no wires cross on top of other wires. Also be careful to not enter "impossible" combinations. For example, if an element is 32 ft long (16 ft each side) with a center height of 50 ft, and you set an end height at 20 ft (impossible), you'll see an Excel error code of "#NUM!" for the slope angle.
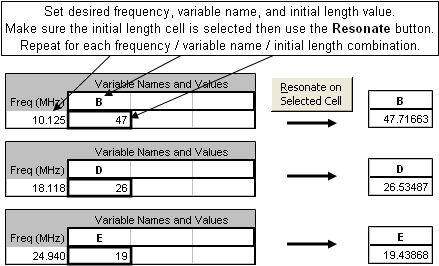
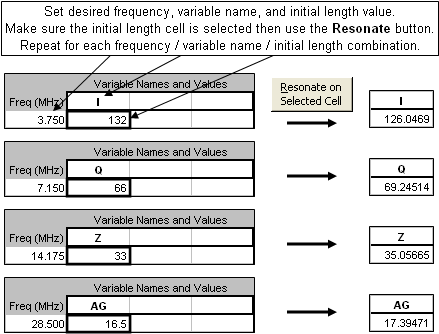
Once you have the model configured as desired the next step is to fine-tune the element lengths to be resonant at your chosen set of frequencies. On the Calculate sheet enter a frequency, the variable name that controls the total length of the corresponding element, and a starting length value. With the length cell selected click the Resonate button. Repeat this process for other frequencies, variable names, and lengths.
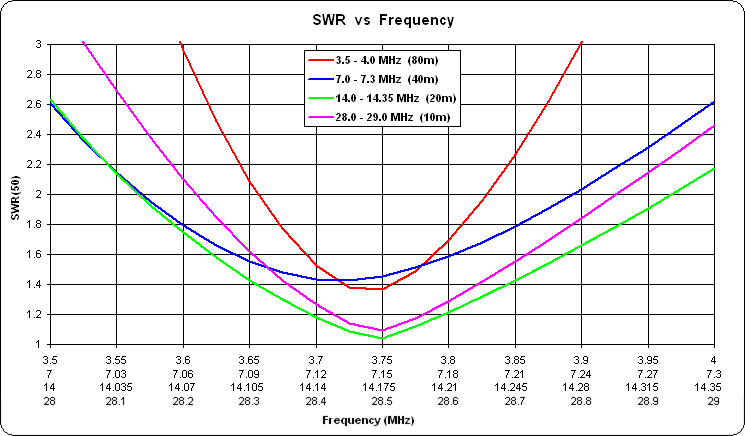
You may then wish to run a frequency sweep across multiple bands to see the SWR patterns. Remember that you are free to do other things such as check email or surf the web while the calculations are running. Assuming you calculated multiple bands at the same time, you can use the
Set/Lock Scales button on the Custom chart sheet tab to "zoom in" on a particular frequency range of interest (discussed more later). This composite chart illustrates the effect.
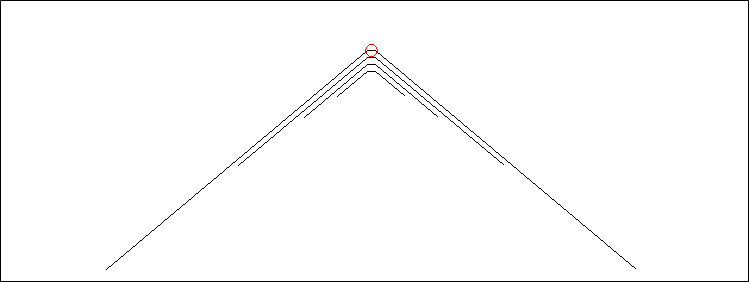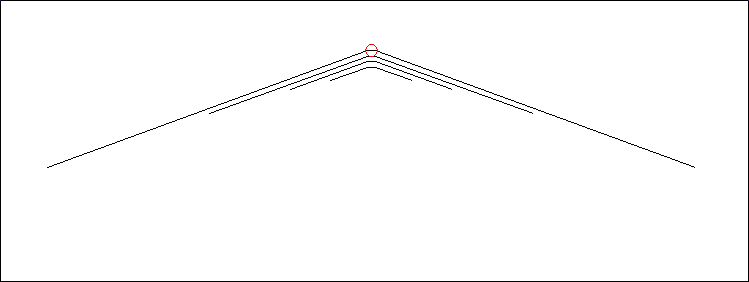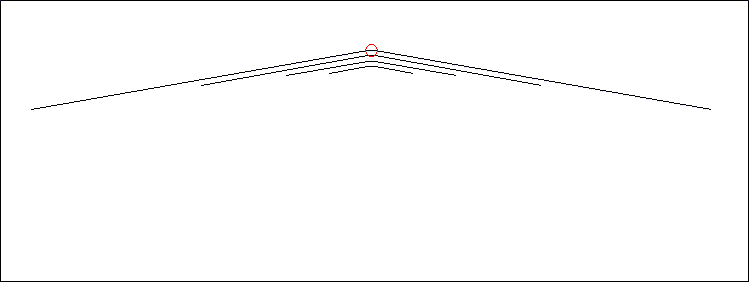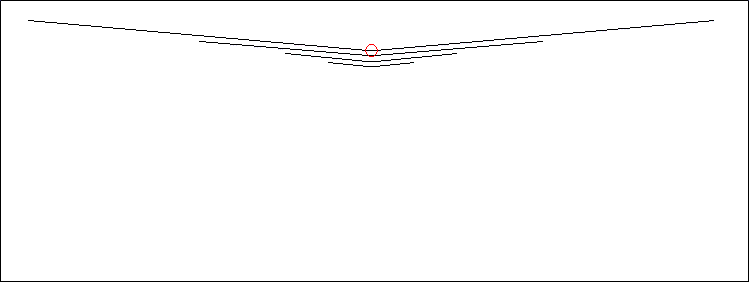
With model "Fan Dipole Parallel Elements.weq" you can easily create a configuration in which the wires are separated by a fixed spacing, typically a few inches to a few feet. This animated gif illustrates that the separation between elements, controlled by a variable, stays constant as the slope angle of the elements is changed.
In both the "Splayed" and "Parallel" fan models the elements are physically separated by a small amount at the centers but are electrically joined by "zero" length (almost) and zero loss NEC transmission lines. This technique was described by L.B. Cebik, W4RNL (SK), see reference below. Making the connection between elements this way, as opposed to building a model with the elements physically connected to a common center wire, results in much better Average Gain Test results, hence more reliable impedance and gain values. As an example, using an exploded view of the splayed element model shown earlier:
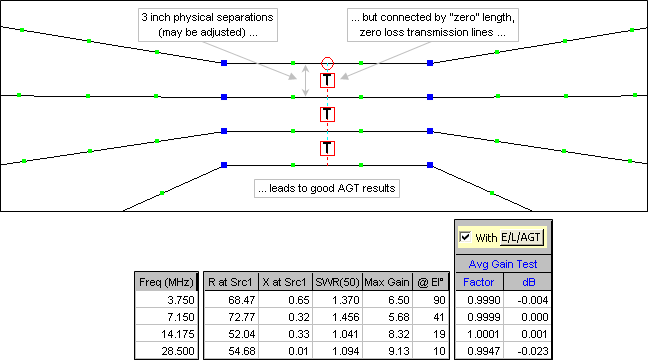
Now compare the above Average Gain Test results with those shown below.
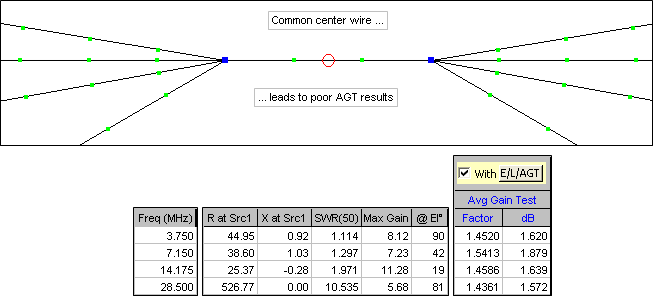
Even after correcting the source resistance and gain by the AGT values, when using a common center wire the results are still unreliable at the higher frequencies.
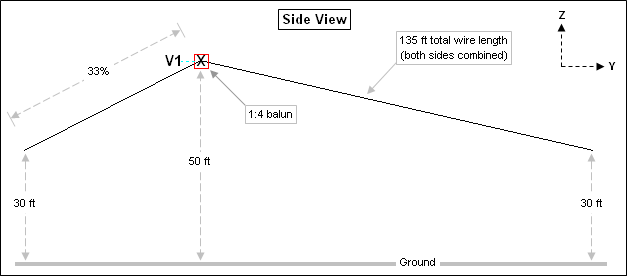
With model "OCF Dipole.weq" you can use variables to set the total wire length and the percent from end for the feedpoint position. As with the fan models you can control the slope angle of both the short and long sections by specifying either end heights or wire angles. An additional variable lets you change the impedance ratio of the balun at the feedpoint, such as 1:4 or 1:6. Here is an example of a typical layout.
And here is the SWR response for this particular configuration. Six frequencies were used for each of 8 bands, 80/40/30/20/17/15/12/10 meters. Using the same number of frequencies for each band means that you can take advantage of the Subsets button on the Custom chart tab to see the response for each band separately (discussed more later), although the illustration below shows all bands together. In this example the max SWR was clipped at 5:1 for plotting so some bands don't show all 6 frequency dots and other bands don't show any dots at all. The straight trace lines connecting groups of dots are merely the "frequency jumps" from one band to the next and can be ignored.

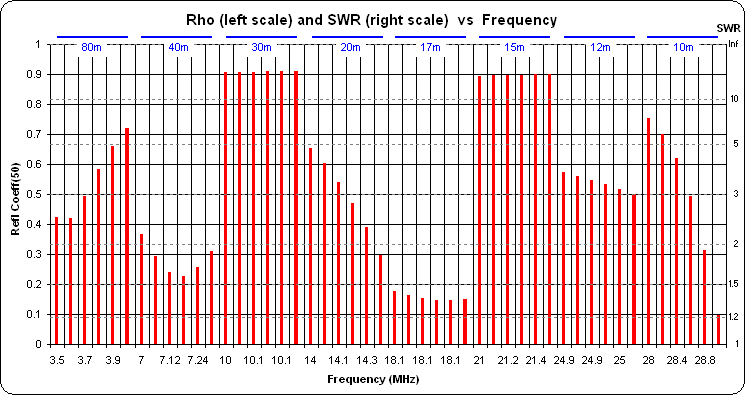
An alternate method to plot SWR is to use "EZNEC spacing" for the Y axis of the chart, which means a reflection coefficient chart with SWR gridlines. (EZNEC SWR charts show only the SWR values but the vertical spacing is per the corresponding reflection coefficient value.) In addition, for the X axis of the chart you can choose
"Frequency - Column" rather than"Frequency - Line" . That eliminates the extraneous straight line traces between the bands. So in the chart below, each band is shown as 6 columns rather than six dots connected by lines. The reflection coefficient (rho) values are on the left vertical scale, the corresponding SWR values are on the right.
When dealing with multiband antennas there is always the question of which frequencies to calculate. Of course you can use something like Start 3.0, Stop 30.0, Step 0.05 MHz but that results in many frequencies of little interest unless you are trying to get a feel for the relationship between SWR dips. An alternative is to calculate groups of frequencies for each band, skipping the frequencies between bands. The Excel "fill handle" makes it easy to enter such groups, as illustrated below.
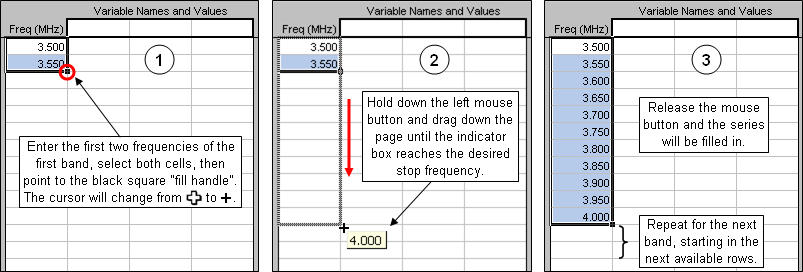
The number of frequencies for each band is determined by the delta between the first two entries for each band. You can use the same step size, say 0.05 or 0.025 MHz for each band, or you can divide each band into the same number of steps. For example (using ITU Region 2 band plans), you might enter
3, 3.55, ... 4 to get 11 frequencies for 80m, then7, 7.03, ... 7.3 to get 11 frequencies for 40m, and so on.When you save the model the current set of frequencies on the Calculate sheet will be saved as well so there will be no need to repeat the entry process the next time you open the model.
After you have calculated several groups of frequencies (that is, several bands) there are two methods available to plot a single band rather than all bands. You can use the
Set/Lock Scales button on the Custom chart sheet tab, setting the min and max of the X axis (typically Frequency) as desired. For example, to plot just the 80m band you could enter min and max values like this.
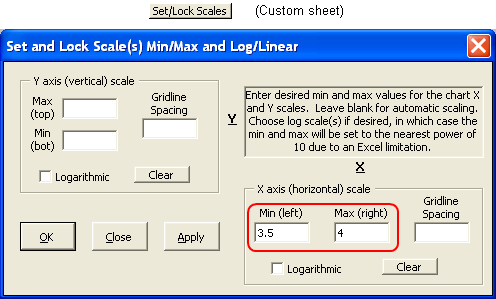
If you click the Apply button the dialog window will stay open so you can easily change to a different min/max (different band). If you click OK the dialog window will close.
There is an alternate way to show separate bands on the Custom chart if you have calculated the same number of frequencies for each band. After all calculations are complete, on the Calculate sheet select (drag through, highlight) just that subset of frequencies that were used for the first band. Then on the Custom sheet click the Subsets button.
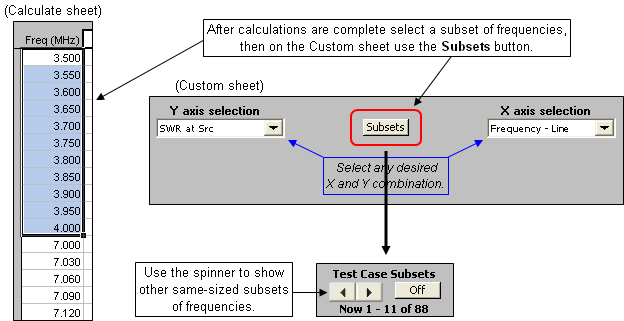
The Subsets button will be replaced with a spinner button. You can use that spinner to advance to other bands, that is, other subsets of frequencies.
References:
Cebik article on using "zero" length transmission lines to connect fan elements:
Dipoles: Variety & Modeling Hazards Zigzag, Fold-Back and Fan DipolesStanford Research Institute paper on fan dipoles:
http://www.rebelwolf.com/HFD.pdfConstruction ideas and other tips for fan dipoles:
http://www.hamuniverse.com/multidipole.html
http://www.hamuniverse.com/ae5jumultibanddipole.html
http://www.hamuniverse.com/w6hdgfandipole.html
http://www.hamuniverse.com/kj4iif1608040fandipole.html
http://ve2xip.cactus.net/?p=1342Construction ideas and other tips for OCF dipoles:
http://www.w8ji.com/windom_off_center_fed.htm
http://hamwaves.com/cl-ocfd/index.html
http://www.buxcomm.com/windom.htm
http://www.balundesigns.com/OCF%20Antenna.pdf
http://www.designerweb.net/downloads/OCF-dipoles.pdfThe "OCF Dipole.weq" model allows a second element to be included. This article explains why you might want to do that:
J. Belrose, VE2CV and P. Bouliane, VE3KLO, "The Off-Center-Fed Dipole Revisited: A Broadband, Multiband Antenna", QST, Aug 1990 (see Appendix in the article)Quick and simple review of sine, cosine, and tangent trig functions, in case you are curious about all the Excel formulas used in the models:
http://www.mathsisfun.com/sine-cosine-tangent.html
Modeling Coupled-Resonator Multiband Antennas
Coupled-Resonator multiband antennas are described in Chapter 7 of the 20th and later editions of The ARRL Antenna Book. See section "The Coupled-Resonator Dipole" written by K9AY. The same information is also found in The ARRL Antenna Compendium Vol 5.
Model CRdipoles.weq may be used for half-wave dipoles and inverted vees. Model CRverticals.weq may be used for quarter-wave ground mounted verticals. (Save the model to your computer then open it from within AutoEZ as explained in Step 3 of the Quick Start guide.)
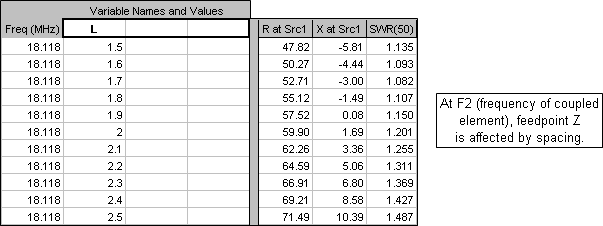
Below is an extract from the Variables sheet for the "CRdipoles.weq" model. The values shown are for a 30/17/12m
C-R dipole, similar to the example developed by K9AY except that he designed for the lower edges of each band and I designed for the band centers of 10.125, 18.118, and 24.940 MHz.
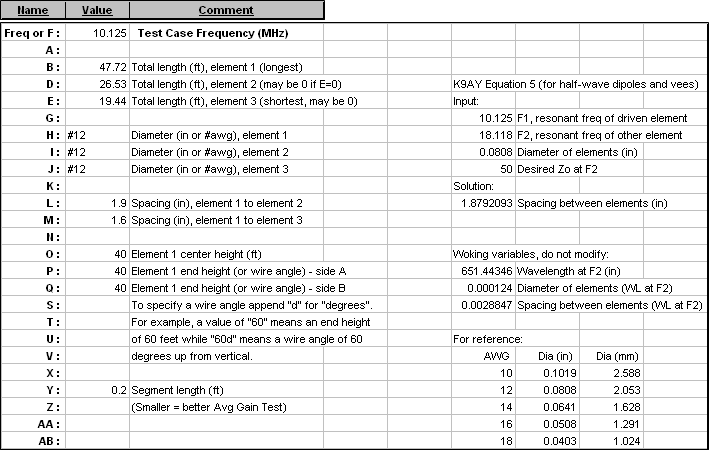
If you would prefer to work with meters instead of feet use the Change Units button (with the "retain formulas" option) before doing anything else. The various comment fields will change automatically. For example, "(ft)" for lengths will be replaced with "(m)". Then set the initial values for element lengths, diameters, spacings, center height, and end heights (or wire angles). For inverted vees, note that the two ends need not be at the same height.
To model only a single coupled element rather than two, set variable E equal to 0. And to model just the primary element, perhaps to compare resonant length or bandwidth without any coupled elements, set both D and E equal to 0.
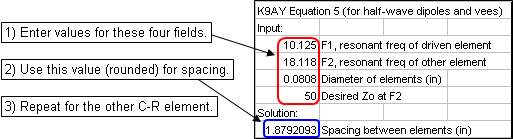
For the element lengths K9AY suggests 477/Freq (in feet) rather than the normal 468/Freq. For spacings you can use the K9AY Eq 5, shown below.

This equation is included in the scratch pad area on the Variables sheet, implemented via Excel formulas.
You can also use the chart shown in Fig A of the Antenna Book sidebar for spacings, but only if the second frequency F2 is in the 10m band. Remember, the spacing is based on conductor diameter in wavelengths at the frequency of the additional resonator. The Fig A chart is for an F2 frequency of 28.4 MHz.
The value you use for variable Y, the segment length, should be fairly small (short segments) in order to obtain good Average Gain Test results and therefore good accuracy with the calculations. The illustration below shows how the AGT result varies with different values for Y. For best accuracy the AGT factor should be close to 1, dB value close to 0.
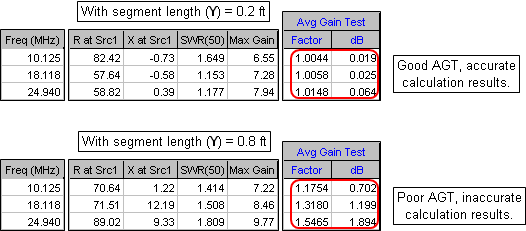
In general you'll want to make Y as small as possible with two restrictions. First, you must not exceed the segment count limit of the EZNEC program type in use. For EZNEC Standard the limit is 500 segments; for EZNEC+ 1500 segments; for EZNEC Pro 20000 segments. The number of segments in the model is shown near the top of the Variables sheet (as well as at the top of the "Segs" column on the Wires sheet). If the number exceeds your limit make Y larger.
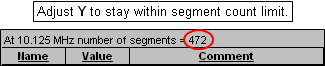
Second, keep in mind the NEC modeling guideline that the segmentation density must be less than 1000 segments per wavelength. To check that, first set the frequency (cell C11) to the lowest value you intend to calculate. That will probably be the lower end of the lowest design band. Then tab to the Wires sheet and make sure that none of the values in the For Information Only "Segs/wl" column (column N) exceed 1000. If any "Segs/wl" values are greater than 1000 make Y larger.

In addition to setting variable values, also make sure that the ground characteristics and wire loss (on the Calculate sheet) and the wire insulation (on the Wires sheet) are all set as desired. For bare (uninsulated) wires use a thickness of 0; dielectric constant is ignored in that case. Insulation values for typical THHN wire were provided by WX7G, thanks!
Once you have the model configured as desired the next step is to fine-tune the element lengths to be resonant at your chosen set of frequencies. On the Calculate sheet enter a frequency, the variable name that controls the length of the corresponding element, and a starting length value. With the length cell selected click the Resonate button. Repeat this process for other frequencies, variable names, and lengths.
You may wish to also fine-tune the element spacings by running a "variable sweep" set of calculations. For example, variable L controls the spacing between element 1 and element 2. At the main dipole (element 1) frequency the resistive component of the feedpoint impedance depends mostly on the antenna height above ground; the spacing will have very little effect. (The reactive component depends mostly on the wire length.)
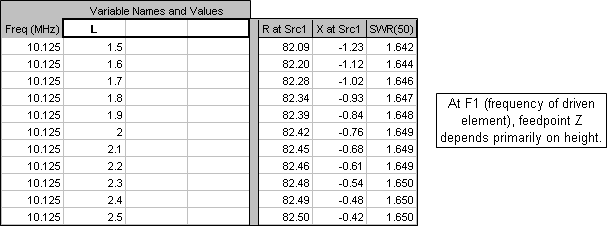
However, at the coupled-resonator frequency (18.118 MHz in this example), different spacings will have a large impact on the resistive component of the feedpoint impedance. And notice that the Eq 5 calculated value (~1.9 inches in this example) is merely a good first estimate to get a 50 ohm resistive component. In this example a spacing of 1.6 inches would be better. (And again, the reactive component can be adjusted by changing the wire length.)
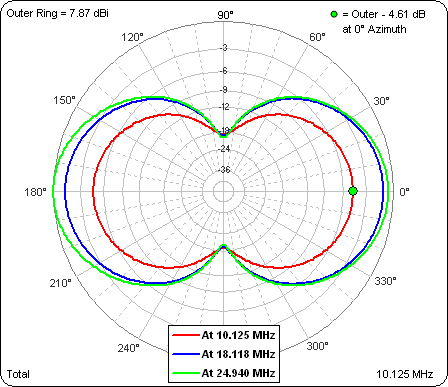
With all dimensions now set you can go on to study other aspects of the model. Here are the azimuth radiation patterns at a 15° elevation angle. (Elements run North-South.) Notice the slight asymmetry. That's because in the model the centers of all the elements lie along a line parallel to the X axis, this is, along a horizontal line, like the elements of a horizontal Yagi. So each
C-R element has a minor director or reflector effect. In the actual installation the elements would no doubt twist slightly toward vertical which would make the azimuth patterns more symmetrical.
And here are the SWR values across the 30/17/12m bands, with element spacings left at the initial Eq 5 values.
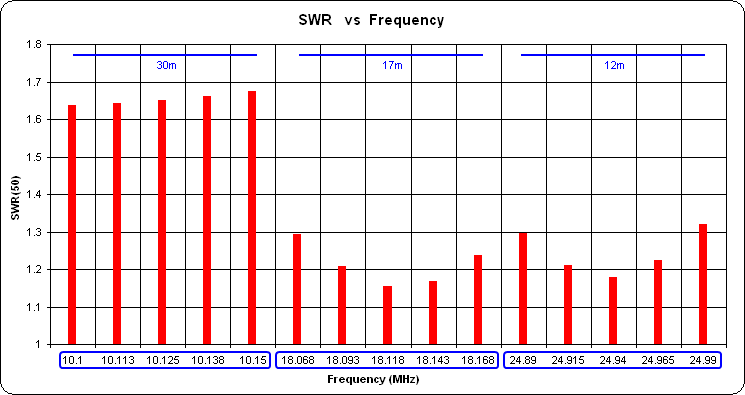
If the spacings had been fine-tuned the SWR at the 17m and 12m band centers would be at or close to 1.
Modeling LPDAs
Recently I assisted an AutoEZ customer with a project involving LPDAs. Along the way I created a couple of model files that might be of interest to others. Both models are found in the "\Sample Models" folder.
Model "LPDA by Tau+Sigma.weq" lets you create an LPDA by specifying a set of parameters including tau and sigma. Here's a screenshot of the Variables sheet tab of the AutoEZ workbook with that model opened.
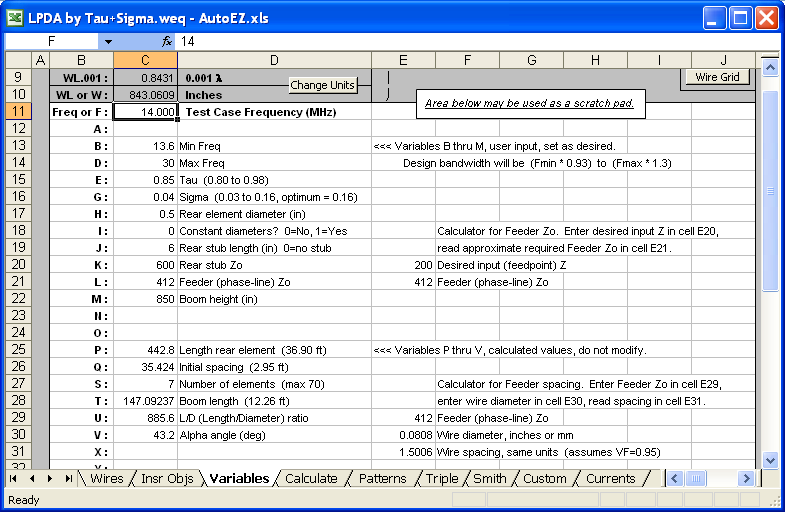
A second model file, "LPDA by Elems+Boom.weq" is similar but lets you set the desired number of elements and the boom length; tau and sigma are deduced. In both cases, by design, the models created will be very close to those produced by the popular LPCAD34 program by Roger Cox, WB0DGF.
Since the parameters can be modified at will and the model is then changed immediately (including a different number of elements if necessary), you can easily run frequency sweeps to compare different parameter sets. Here's a sweep comparing two tau/sigma combinations.
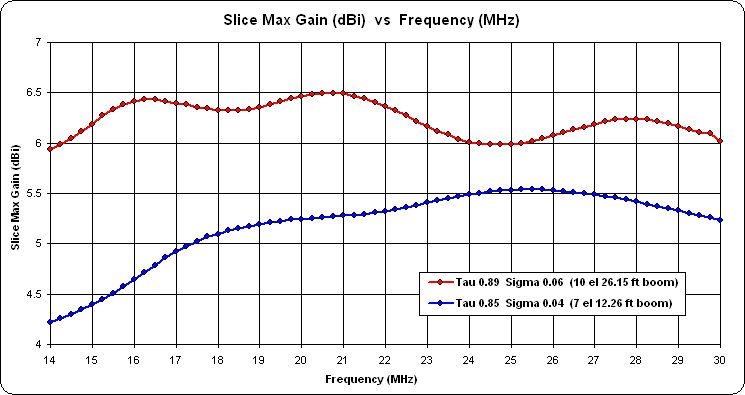
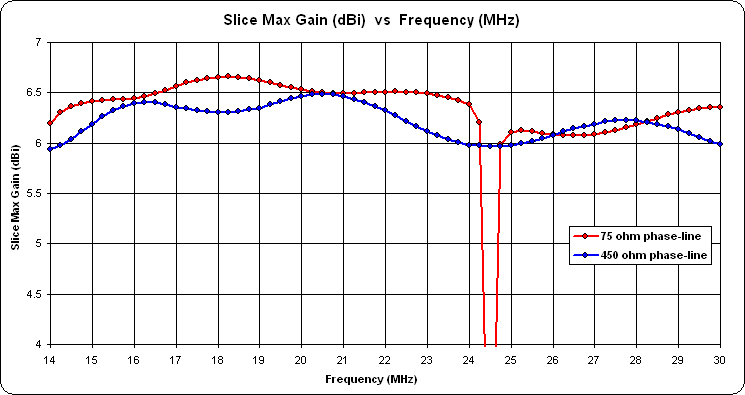
And here's one comparing different phase-line Zo values, both for the same tau/sigma (0.89/0.06). Note the aberration between 24 and 25 MHz when using a 75 ohm phase-line. That spike can be moved to a different position, perhaps to a frequency not to be used, by changing the rear stub.
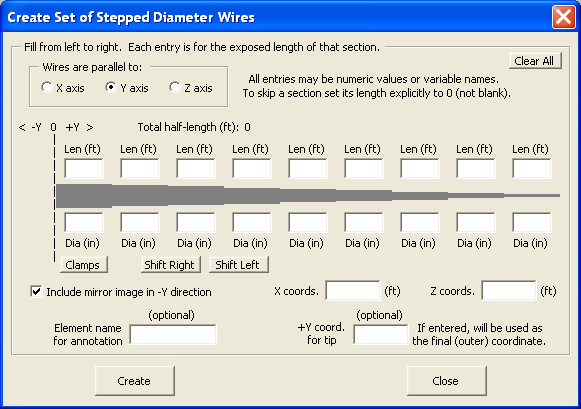
Once you have the design finalized you may be tempted to use the AutoEZ "Create Set of Stepped Diameter Wires" dialog to replace each cylindrical element with a "taper schedule" set of wires representing your proposed physical construction.
Unless you are using EZNEC Pro/4 with a NEC-4 engine you probably do not want to do that for LPDAs. When a model contains "stepped diameter" sets of wires, EZNEC (except Pro/4) will attempt to use the Leeson correction to convert each set back to a cylindrical (mono-taper) equivalent. However, the correction can only be applied when the element is within about 15% of resonance. With LPDAs, at any given frequency only some of the elements will be within that resonance range and hence can be "Leeson corrected". Other elements will be left as stepped diameter, producing inaccurate results under NEC-2.
Here's a comparison.
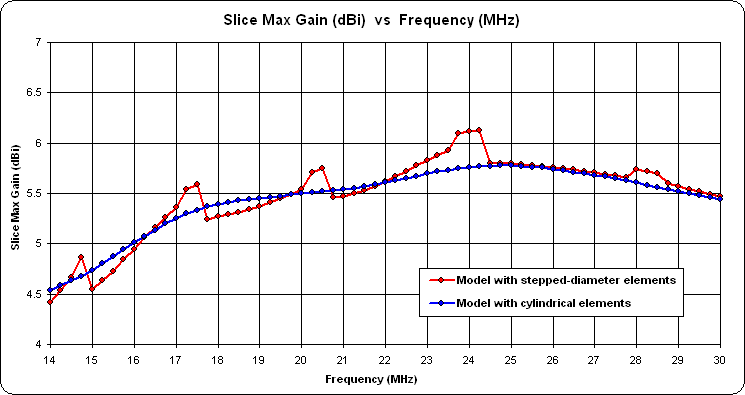
Note that this caution does not apply to single-band Yagis. In that case all the elements can normally be "Leeson corrected" without problems.
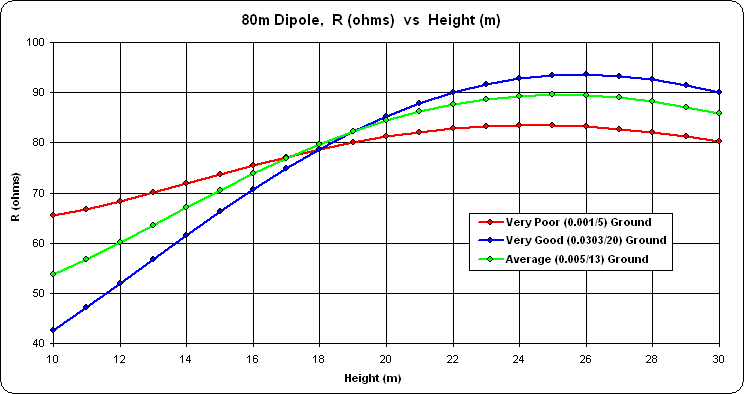
Feedpoint R vs Height
A question was asked about how the feedpoint resistance for a dipole varies with height and different ground conditions. A simple 80m dipole was modeled at 3.680 MHz with each leg 19.647m long. That leg length results in resonance when the antenna is 20m above real/average ground. Here's the model.
The height was varied from 10 to 30 meters using three different ground conditions. On the Custom chart tab the plot choices were set as "R at Src" on the Y axis and "Variable 1" on the X axis. "Variable 1" is the first of up to three variables that you can change at one time on the Calculate sheet, which in this case is the "H" variable that controls the antenna height.
For each ground condition the Snapshots button was used to "capture" the trace. Then the ground condition (second drop down under "Ground Type, Char" on the Calculate sheet) was changed and a Calculate All Rows was done again.
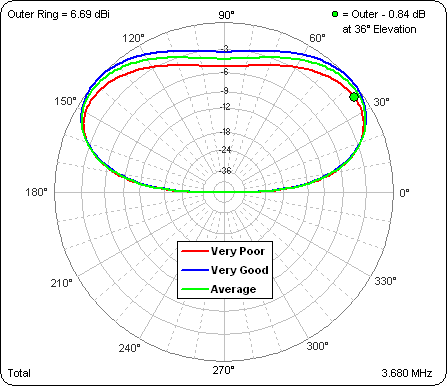
A follow-up question was asked about how the different ground conditions affect the takeoff angle (TOA) at 30m. Even at a height of 30m the elevation pattern for an 80m dipole is still very broad. This is the pattern for the three different grounds.
A better way to look at things in this case is with a rectangular rather than polar pattern:
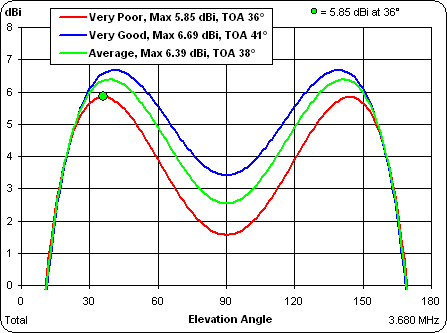
The TOA actually gets higher (from 36° to 41°) with better ground. Normally that's not desired but in this case it's because the max gain also goes up (from 5.85 dBi to 6.69 dBi).
Designing Delta Matches
The delta match is discussed in all editions of The ARRL Antenna Book, see "Delta match" in the book index. To duplicate the scenario shown in the book, create a dipole made from three wires such that the overall length is L with an adjustable center section of length A. Then add two additional wires for the delta match, dropping down for a distance of B. If the dipole is 50 feet above ground the (X,Y,Z) coordinates for the various wire ends would be as follows, assuming the antenna lies in the YZ plane. (For convenience, links to sample AutoEZ format models are included below.)
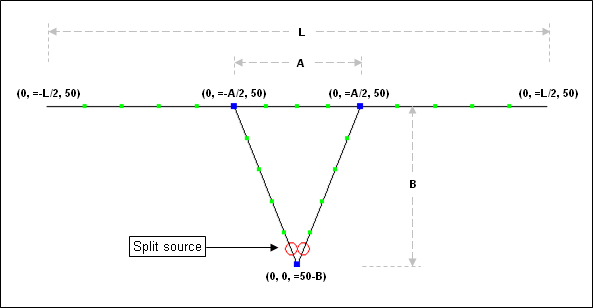
Put a split source at the point where the feedline is to be attached. Use the SWR Zo button on the Calculate sheet to change the SWR reference impedance from the normal 50 ohms to 600 ohms.
To match an HF dipole to 600-ohm open wire transmission line the Antenna Book suggests a value of 0.120 λ for A and 0.150 λ for B. On the Variables sheet give A and B these initial values (converted to feet) and give L an initial value of 468/Freq.

Now optimize all three variables to produce the lowest possible SWR(600) at the feedpoint.
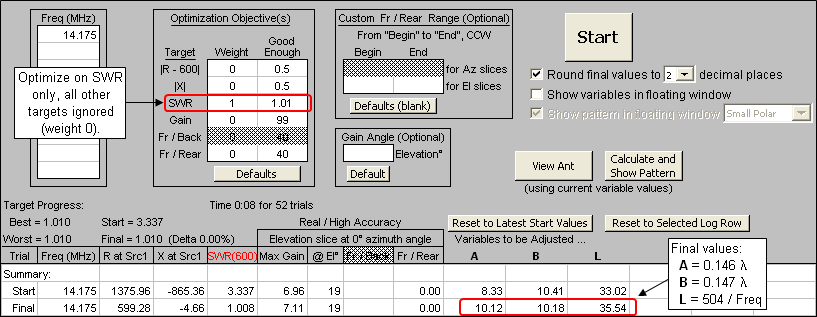
With the optimized values determined you'll probably want to run a frequency sweep to see the bandwidth of the matching arrangement.
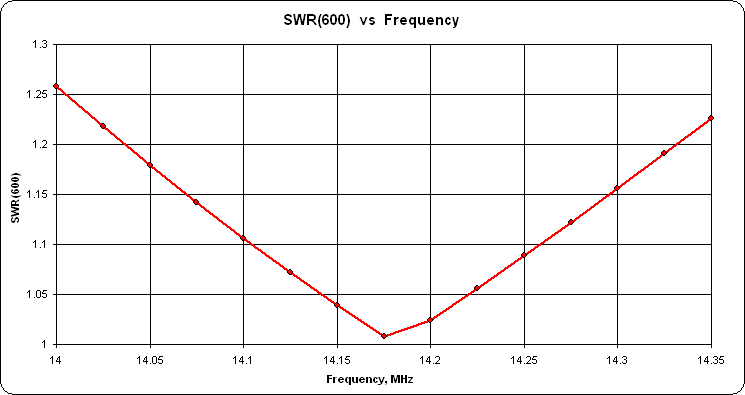
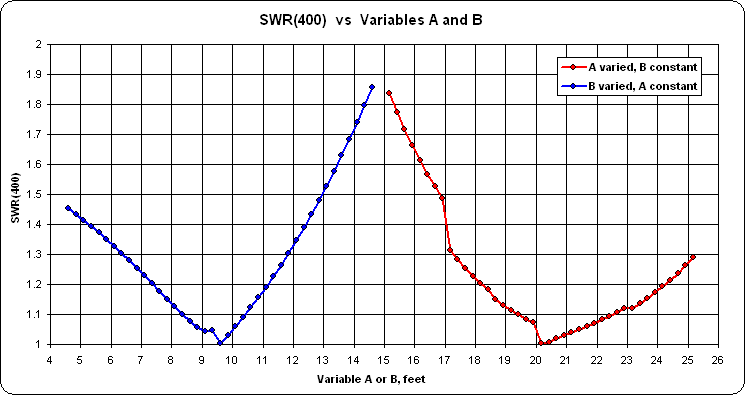
You may also wish to run "variable sweeps" on A and B to study the sensitivity of small changes in each. Below are the results of varying A from 5 to 15 ft while B is held constant at the optimized final value, then varying B while A is held constant, in both cases at a frequency of 14.175 MHz. (Note the different range for the SWR scale compared to the previous chart.)
In this case (but not all cases) A is much more sensitive than B, a fact to remember when building and adjusting the physical antenna system.
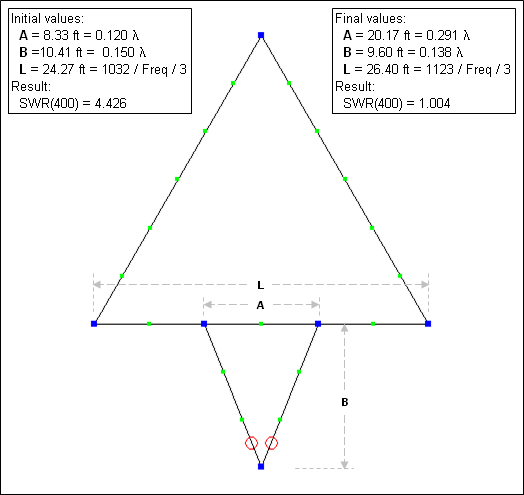
Here's another example, this time for a triangular loop with the center at 50 feet, to be matched to 400 ohms which is the approximate Zo for commercial "450 ohm" window line. Start by using the "Create Loop" dialog to quickly build the three wires of the loop, specifying L as the length for each side. AutoEZ will create the necessary (X,Y,Z) coordinates such that the center of the loop will stay at 50 feet as L is varied.
As with the dipole, modify one of the sides to include a center section of length A. Add two additional wires for the delta match. Use the SWR Zo button to set the SWR reference impedance to 400 ohms.
For antennas other than dipoles and/or for transmission lines with a characteristic impedance other then 600 ohms, the Antenna Book offers no guidance other than saying that A and B must be found by experimentation. Lacking any better guess, use the same initial values for A and B as with the dipole. For L, use an initial value of ⅓ of 1032/Freq or 24.27 ft (see Antenna Book index "Loop, One-wavelength"). Then optimize to adjust A, B, and L for the lowest SWR(400) value.
And here's the same kind of sensitivity study for A and B. In this case each was varied by ±5 ft on either side of the optimized final value.
The two models below can be used with the free demo version of AutoEZ which is limited to calculations of no more than 30 segments. (Note that you can't just click on the link to open the model. Save it to your computer then open it from within AutoEZ, as explained in Step 3 of the Quick Start guide.)
DeltaMatchDipole.weq
DeltaMatchLoop.weqBecause of the reduced number of segments, with the Loop model you will see EZNEC segmentation check warnings (but not errors). If you have the full version of AutoEZ, not the demo, you may wish to increase the segmentation density of both models by using the AutoSeg button on the Wires sheet. Try 100 segments per wavelength, odd or even, all wires. That will put the "effective" position of the feedpoint closer to the actual apex of the delta match wires and will produce more accurate results.
With both models, the Average Gain Test shows that accuracy is slightly compromised due to the acute angles of the delta match wires.